虚短设计,虚短和虚短适用条件

运算放大器在信号的采集、放大等各种应用中非常广泛，其应用电路也非常多，因此虚短设计我们特地针对运算放大器的各种电路的实现、参数和一些关键的特性做了总结，以供各位小伙伴查阅。

在模拟电路中，为了分析方便，通常将集成运放视为理想的集成运放，虽然在理论上这样会带来误差，但是仍然在工程的允许范围之内。理想的运算放大器其开环差模放大倍数为∞。也就是说，即使两输入端加上无穷小的输入电压，也足以让运放工作在非线性区。也就是说运放开环时只有两种输出电压虚短设计：±Uom。但是我们需要让运放为我所用，就需要让运放工作在线性区域，就需要引入一个重要概念：深度负反馈。

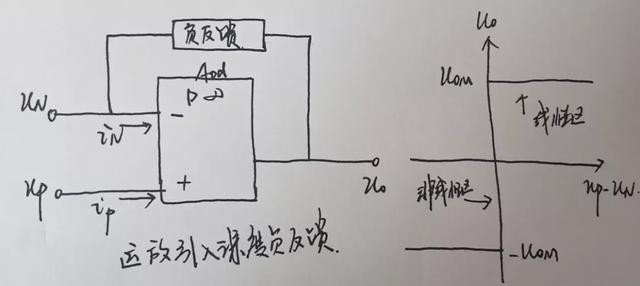
在上面我们引入了深度负反馈，这是利用运放组成运算电路的必要条件。从运放的实际电路结构上来说，运算电路实际上是一个高开环放大倍数、深度负反馈的直接耦合放大电路。

在运放电路而言，利用“虚短”和“虚断”和KCL定律即可计算出输出电压Uo和输入电压Ui之间的数学关系。但是在实际应用中过于复杂，因为我们总结出几大类常用的运放应用电路。

1、电压跟随器

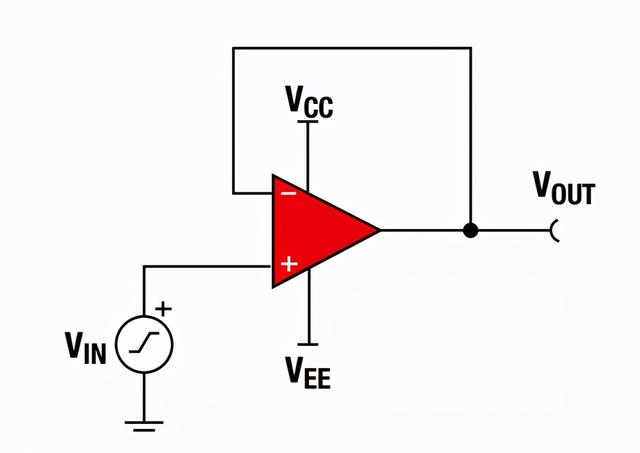
如上图所示，利用“虚断”“虚短”的概念我们很容易的计算出输出电压Uo=Ui

在该电路中，输出电压跟随输入电压一起变化，故称之为电压跟随器。电压跟随器的关键特点是：输入电阻大、输出电阻小。通过这一特性我们通常将电压跟随器用作缓冲器，对后级电路而言，通常就相当于一个恒压源，可以起到一个隔离的作用。

2、同相比例运算电路

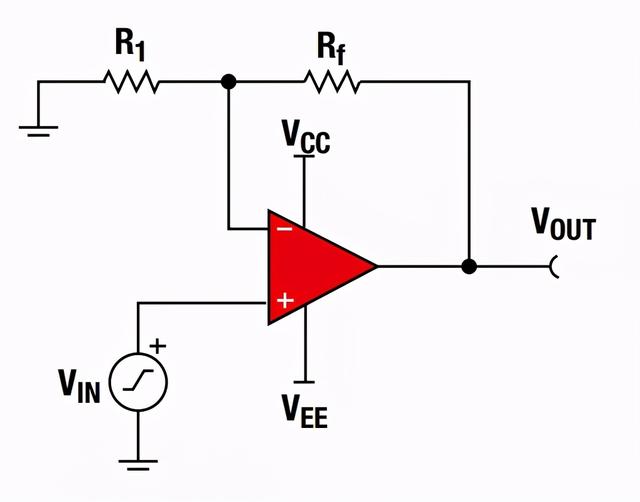
上图为同相比例运算电路，输入信号直接加在运放的同相输入端，利用“虚短”和“虚断”可以计算出其增益如下，其中因为输出电压Uo和Ui的相位相同，所以我们称为同相比例运算。

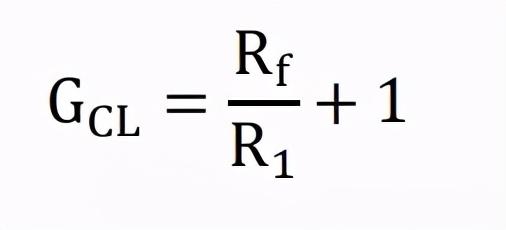
3、反相比例运算

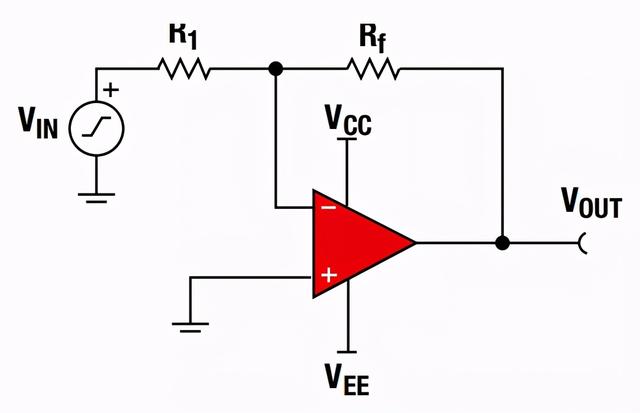
通过计算可以计算出输出增益为，通过如下的计算公式可以知道输出电压和输入电压的相位相反，所以我们称之为反相比例运算电路。

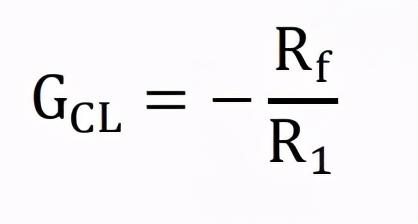
4、差分比例运算电路

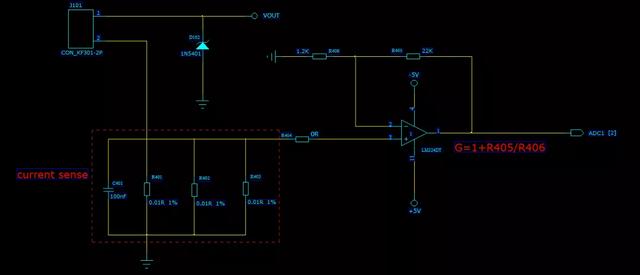
通常我们用比例运算电路去放大各种电压电流信号，比如同相比例运放，我们可以用该电路去做电流检测，如下图所示，但是该电路通常采样信号幅度较大，因此对抗干扰能力的要求并没有那么高。而还有一种场景是传感器需要采样一些非常微弱的信号（零点几毫伏级别），这时候就需要用到差分比例运算电路。

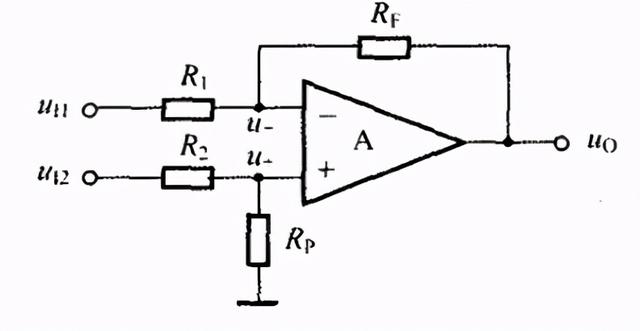
如下图为差分比例运算电路的一般形式，为了保证输入端电路的对称，需要满足的条件是：

R1//Rf=R2//Rp

通过理论计算，最终得到输出电压和输入电压的关系为：

Uo=-Rf/R1(U1-U2)

即输出电压和输入电压的差值成比例，所以我们称为差分比例运算放大器。

5、加减法运算电路

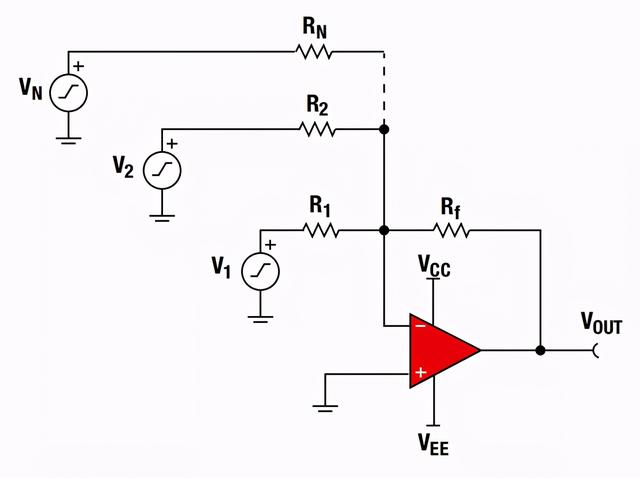
实现多个信号按照一定比例求和或者求差的电路称之为加、减法运算电路，若多个信号经过电阻全部作用于集成运放电路的同一输入端，则组成加法运算电路；若多个信号经过电阻分别作用于集成运放的两个输入端，则组成减法运算电路，如下图电路所示为反向加法运算电路和同向加法运算电路：

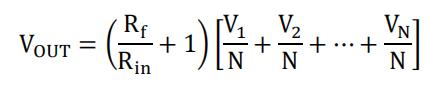
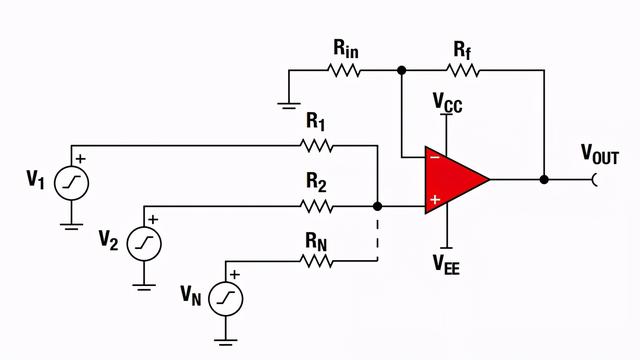
6、具有Cf滤波器的放大器

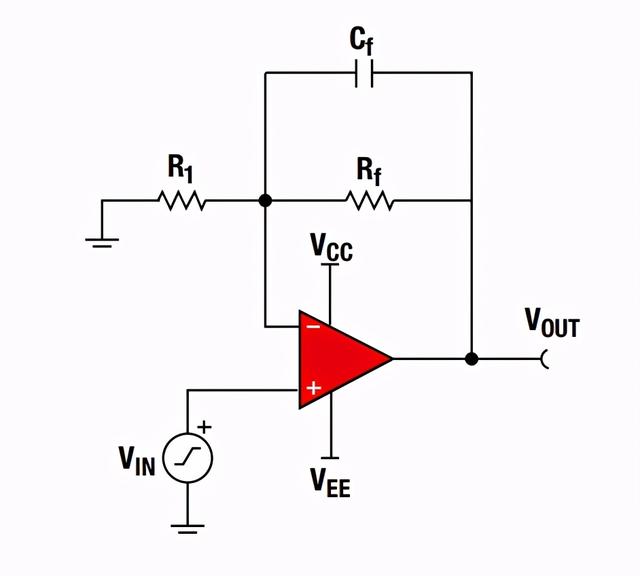
在运放的实际应用电路上，通常会在反馈电阻上增加Cf滤波器，其主要的作用如下：

①做相位补偿，增加相位余量，可以提高运放的稳定性，防止自激；

②起到低通滤波器的作用，因此加上Cf电容会减小运放的带宽。

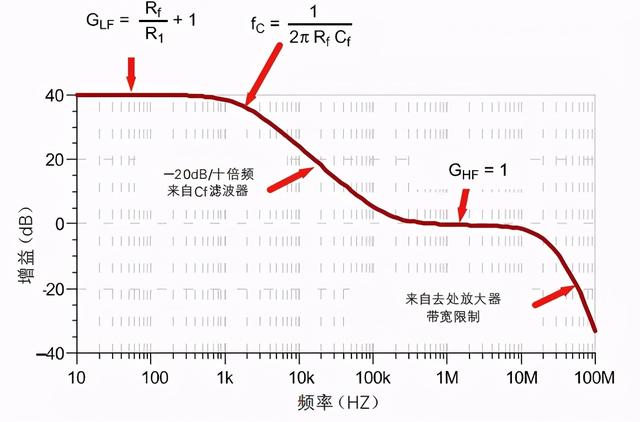
如上所示的公式为加Cf滤波器的运放在高频和低频两个场景下的增益，下图为该同相运放的频率响应曲线，带Cf滤波器的反向放大器同理。

7、积分/微分运算放大器

积分电路和微分运算电路在自动控制系统中，常常被用来对控制信号进行积分和微分调节，此外，它广泛地用于各种非正弦波的产生和变换：例如在非正弦波产生电路中，用作时延电路，在波形变换中，将方波变为三角波：A/D转换中，将电压量转换为时间量等。

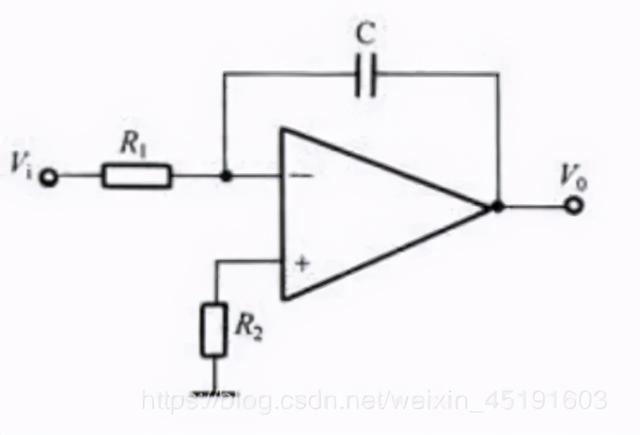
将反向比例运算电路的反馈电阻Rf用电容C替代，就构成了反向积分运算电路，该电路的分析同样使用“虚短”、“虚断”即可计算出来。

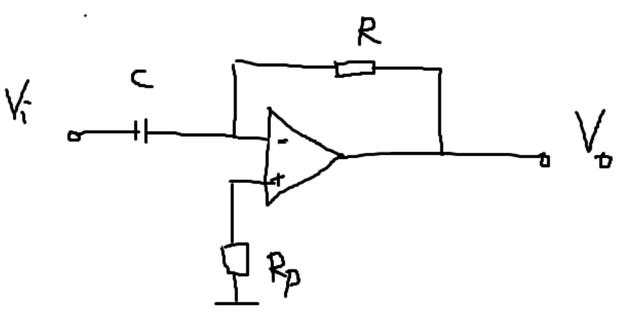
将反向比例运算电路中输入端的电阻换成电容，就构成了微分运算电路：

内容转载自 网络，仅供学习交流使用，如有侵权，请联系删除。如果你还想了解更多关于电子元器件的相关知识及电子元器件行业实时市场信息，敬请关注微信公众号 【上海衡丽贸易有限公司】